When looking at culture-driven population dynamics, a common assumption is that there’s a positive feedback between cultural evolution and demographic growth. The general prediction, then, is for unlimited growth in population and culture. Yet models based on these assumptions tend to ignore important aspects of cultural evolution, namely: (1) cultural transmission is not perfect; (2) culture does not always promote population growth. Ghirlanda et al (2010) incorporate these two features into a model, and arrive at some interesting conclusions. In particular, they argue those populations maintaining large amounts of culture may run the risk of extinction rather than stability or growth.
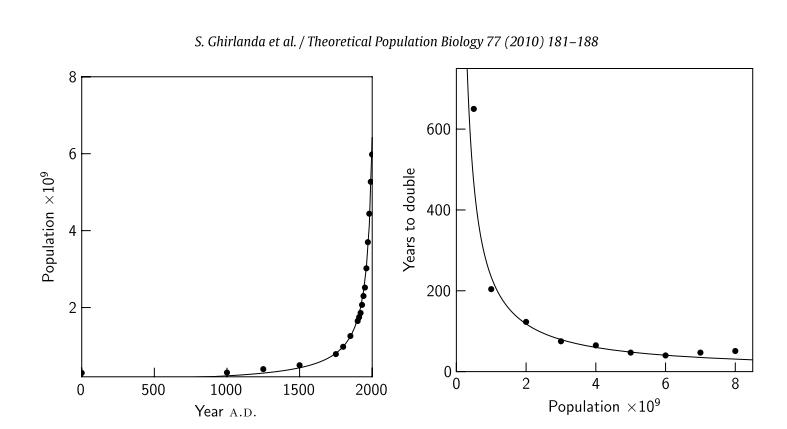
The first factor to consider is population growth. Above are two graphs: the left shows the pattern of human population growth from 0-2000 AD; the right shows time taken for the population to double. As we can see, the doubling of population growth is taking place far more quickly as time progresses; that is, we’re looking at a period of exponential growth (even though most models of human population dynamics are intended to account for hyperbolic growth). Mathematical attempts to capture this data noted that humans are defying the Malthusian regulatory mechanisms that limit growth in animal populations. Estimates by Van Foerster et al (1960), for instance, predicted human populations would become unsustainable in 2025. Generally, though, the doubling time of human population growth is apparently stabilizing around a value of 40-50 years — aspects such as reduced fertility and increased standard of living are allowing some countries to slowdown. But even in this instance, some estimates place the human population at around 8–11 billion by 2050 AD, which are normally obtained by extrapolating from current demographic trends (or relying on projected income and relating this as a determining factor in population growth).
So what happens when you account for feed-back between population, cultural and environmental dynamics?
Ghirlanda et al begin by looking looking at human population dynamics as modifications of population dynamics models based on the logistic equation:
Here, n is population size while 
is its rate of change, r is the population’s intrinsic growth rate, and k is the environmental carrying capacity. Under this equation, an initially small population grows until it reaches the carry capacity, which is normally due to the finite number of resources becoming scarcer. In the case for most models of human population growth, the general assumption is that technology, social organisation, and other features of culture allow humans to increase this environmental carrying capacity. The tendency, then, is to assume cultural and technological innovation is the major driving force behind human population growth. To some extent this makes sense: the creation of technology sustains a large population, which subsequently produces more technology — creating a positive feedback loop. But as the authors note:
The outcome of this model, as mentioned above, is very fast (hyperbolic) demographic and technological growth. The model shows that the interaction between culture and demography is crucial to understand human population dynamics, but ignores several potentially important factors. For instance, it only considers culture that promotes population growth (technology), and it assumes that technology is perfectly transmitted between generations.
Even in cases where technology promotes population growth, there are instances where cultural traits may act as inhibiting mechanisms. For instance, Ghirlanda et al point to how individuals frequently invest resources in non-reproductive activities, such as higher education. Also, a cultural trait that at one stage promoted population growth may later find itself, through over-exploiting a particular resource, as severely limiting factor:
The consequences can be catastrophic, such as the Irish Great Famine of 1846-1850 AD, when a fungus destroyed the potato crops on which over half of Irish population relied. Potato farming had previously been a very productive technology, yielding the same nutritional value of corn for one third of the cost, thereby allowing Ireland to export larger quantities of wheat.
To factor in these features, the authors modify the above logistic equation by inserting α to describe the impact culture has on the environments carrying capacity, which they deem as the subsistence potential of culture:
In the brackets, the u and v simply capture instances where culture promotes and inhibits growth as both different yet interacting dynamical variables. By varying the impact of culture on carrying capacity, α, and the corruption rate of culture, θ, with the initial population size being n = 1, the authors arrived at three long-term outcomes (shown in the figure below):
Broadly, the three long-term outcomes are stable equilibrium (grey areas), unlimited growth (white areas), and extinction (black areas). In the stable equilibrium, the population can be larger (dark grey) or smaller (light grey) than a population without culture. To reach a stable equilibrium, the subsistence potential of culture, α, must be small, and is practically independent of the corruption rate, θ. The authors note that this is basically the equivalent of a population with relatively inefficient technology. Meanwhile, unlimited growth happens when “Population size, as well as the difference between growth-promoting and growth-inhibiting culture, increases exponentially with time”. Lastly, a population goes extinct when the corruption rate and the subsistence potential of the culture are large enough:
Under such conditions, growth-promoting culture initially increases, leading to an increase in population size, but is eventually overcome by growth-inhibiting culture and therefore population collapse. When α is large, collapse can be preceded by a very large increase in population (trajectory 3), when α is small the initial increase is modest (trajectory 1).
As I mentioned at the start, human population is growing exponentially. But why, prior to 1960 AD, do we see a growth rate faster than exponential? One assumption is to assume culture augments both the environment’s carrying capacity and the intrinsic rate of population increase in a linear fashion. An alternative proposal is that the rate of cultural innovation is increasing faster than linearly with population size. Ghirlanda et al point to several measures of innovation: e.g. the number of people employed in research and development activities. This has clear implications for studies predicting a stabilisation of the human population at around 8-11 billion in 2050. First, these projections gloss over sustainability. For instance, even in a fixed population of individuals, resources can be exploited in an unsustainable fashion. Second, it’s not guaranteed that fertility will decline everywhere in the world in a similar manner to that of industrialised nations. A change in beliefs may encourage high fertility or, assuming fertility is tied to income, could increase during a global economic recession (although there are studies showing fertility decreases in the developed world during a recession).
The clear message is fairly consistent with most intuitions:
[A] population capable of maintaining a large amount of culture, including powerful technology, runs a high risk of being unsustainable… [However], assessing the sustainability of culture-driven population dynamics requires a deeper understanding of cultural evolution in at least two areas: ideas about reproduction, e.g., concerning the preferred family size, and ideas that influence resource use, such as beliefs about acceptable energy consumption.
Citation:
Ghirlanda, S., Enquist, M., & Perc, M. (2010). Sustainability of culture-driven population dynamics☆ Theoretical Population Biology, 77 (3), 181-188 DOI: 10.1016/j.tpb.2010.01.004
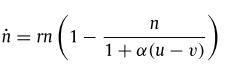
This assumption is incorrect. Cultural features, especially fossil fuel inputs into agriculture, do not increase carrying capacity (K). Rather, they allow human population to exceed K. Populations that exceed K inevitably crash. The more they exceed K the harder they crash. Human population exceeds K by orders of magnitude above and beyond what any large vertebrate population ever has exceeded K previously. When human population crashes, likely triggered by resource depletion and other environmental stressors, it is almost certain to crash all the way to extinction. “Cultural features,” then, rather than being seen as a means for increasing K, become the very means of bringing about and virtually ensuring human extinction.
If you look at the modified logistic equation, then you have ways in which culture both promotes growth and inhibits growth through modifying the carrying capacity. Perhaps we are exceeding our carrying capacity at the moment. Still, it does not mean we cannot increase our carrying capacity in the future (imagine some sci-fi like scenario where we end up harnessing the resource potential of other planets). But I’d always be careful about making statements like: “… bringing about and virtually ensuring human extinction.” Unless, to keep with the sci-fi scenario, you have a time machine and know that we’re doomed.
two points.
First, it seems to me that it can be witted down to the pretty uninteresting conclusion of bad or unlucky culture can cause problems. If you have more bad culture than good culture, your screwed. I guess it’s an improvement over the other none-to-earth-shattering findings of technology/culture allowing for an increase in the population.
Second, from a technical standpoint, they force the lambda (or the loss of culture) to be the same for good culture and bad culture. presumably lambda for good beneficial culture should always be lower than the lambda for bad culture, which might make for a much wider zone of non-extinction.
@darwinsdog would you say that bio-diversity increases the sustainability of an ecosystem? That’s another way to say that carrying capacity can be increased. Culture could, even if it currently doesn’t, promote bio-diversity which would increase carrying capacity.