Author: Sean

As the Evolang deadline approaches, Bart de Boer and Tessa Verhoef have announced a workshop on the evolution of signals, speech and sign which will take place just before the main conference. The deadline for papers to the workshop is October 10th.

We are looking for contributions that address the evolution of modern humans’ abilities to produce, perceive and learn the extended range of (combinatorial) signals that form the physical basis of human language. Signals in our definition form the physically observable manifestation of language, and they can exist either in the articulatory-acoustic modality (speech) or in the gestural-visual modality (signs) and perhaps in other modalities.
The event is intended to be complementary to the main conference in the sense that we look for contributions that explicitly focus on future research. We therefore seek contributions that not only present research results, but that for example also explore possibilities of interaction between fields, that pose new research questions or that make an inventory of areas in which research may be lacking.

On the weekend I did an analysis about a recent paper by Caleb Everett linking altitude to the presence of ejective sounds in a langauge. In this post I look at the possible effects of contact and population size.  I find that controlling for population size removes the significance of the link between ejectives and elevation.

In a comment on the post, Chris Lucas suggested that languages at higher altitudes might be more isolated, and so less subject to contact-induced change:

“contact tends to make languages lose ejectives, if they ever had them. The reasoning here would be that a language’s having (contrastive) ejectives implies that it has a large consonant inventory, which implies that it does not have a history of significant numbers of people having learnt it as a second language, since this tends to lead to the elimination of typologically rare features.”

We can test this in the following way: We can get a rough proxy for langauge contact for a community by counting the number of languages within 150km (range between 0 and 44).  If we run a phylogenetic genralised least squares test, predicting the presence of ejectives by elevation and number of surrounding languages, we get the following result (estimated lambda = 0.8169142 , df= 491, 489):

	Coefficient	Std.Error	t-value	p-value
Elevation	0.00004514	0.00001655	2.728177	0.0066 **
No. surrounding langs	-0.00312549	0.00147532	-2.118507	0.0346 *

While elevation is still significant, the number of surrounding languages is also a significant predictor (the effect size is also greater).  The greater the number of surrounding languages, the smaller the chance of a langauge having a ejectives.  This fits with the idea that contact induced change removes ejectives, rather than air pressure being the only cause.   In the graph below, I’ve plotted the mean elevation for languages with and without ejectives, comparing languages with a neighbour within 150km and languages without a neighbour in 150km.  The effect is stronger in the group with neighbouring languages (right), which would fit with languages loosing ejectives due to contact.

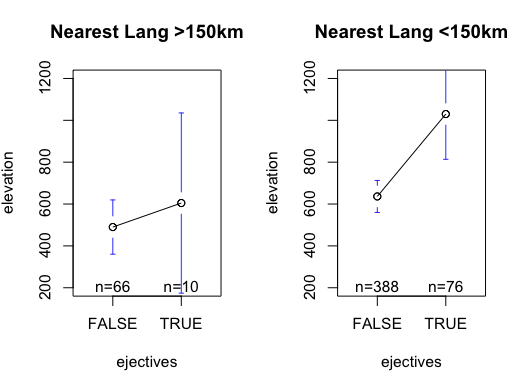
However, it’s not quite so simple, since we have to take into account the relative relatedness of languages.  If we count the number of distinct language families within 150km, then the significance goes away:

	Coefficient	Std.Error	t-value	p-value
Elevation	0.00003893	0.00001645	2.366329	0.0184 *
No. surrounding families	0.00348498	0.0074656	0.466806	0.6408

What about another proxy for contact, like population size (as used by Lupyan & Dale, 2010)?  I took speaker populations from the Ethnologue and ran another PGLS:

	Value	Std.Error	t-value	p-value
Elevation	0.00001786	0.00001962	0.910439	0.3632
Log population	-0.0110823	0.00817542	-1.355564	0.1761

Now we see that neither variable is significant, though larger populations tend not to have ejectives.  That is, by controlling for linguistic descent and population size, the correlation between elevation and ejectives goes away.

In fact, a simple logit regression predicting elevation by elevation and log population results in the following:

	Estimate	Std.error	z-value	Pr(>|z|)
(Intercept)	-0.6579524	0.3874394	-1.698	0.089469 .
Elevation	0.0003757	0.0001665	2.257	0.024014 *
Log population	-0.327502	0.0920464	-3.558	0.000374 **

We can see that, even if we don’t control for phylogeny, population size is a better predictor of ejectives than elevation (although Everett uses several measures of altitude).

I also wondered if the distance to the nearest language could be a proxy for contact.  Let’s put all the variables into one regression.

	Value	Std.Error	t-value	p-value
Elevation	0.0000257	0.00001988	1.290864	0.1976
No. surrounding languages	-0.0069331	0.00278402	-2.490329	0.0132 *
Minimum distance to nearest language	-0.0001173	0.00011222	-1.04528	0.2966
Log population	-0.011234	0.0081391	-1.380251	0.1684

Here we see that the number of surrounding languages is still a significant predictor of the presence of ejectives (although using the number of surrounding families doesn’t work), but elevation is not.

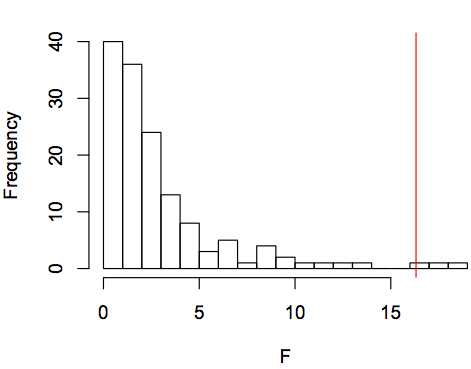
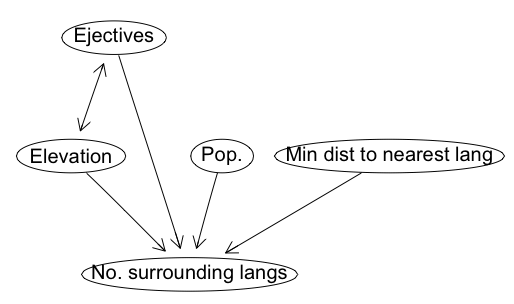
We can build the most likely causal graph (see my post here) for the data above.  This ignores the phylogenetic relatedness of langauges, but allows us to explore more complex relationships between all the variables.  Below, we see that elevation and ejectives are still linked, as Everett would predict.

The stats I’ve presented here are just rough explorations of the data, not proof or disproof of any theory.  Here are some issues that are still unresolved:

• What about the distance from high-elevation areas, as used in Everett’s paper?
• Are the proxies above reasonable?
• What is the likelihood of keeping ejectives versus losing them during contact?
• In the analyses above, I’m not controlling for geographical relatedness, this could be done by selecting independent samples or Mantel tests.
• There are links between phoneme inventory size, the geographic area a langauge covers, morphology and demography (see James’ posts here and here).  What is the best way to approach the complex relationships between these features?

Of course, laboratory experiments or careful idographic work could address these issues better than more statistics.

A recent paper in PLOS ONE by Caleb Everett looks at whether geography can affect phoneme inventories.  Everett finds that language communities that live at higher altitudes are more likely to have ejective sounds in their phoneme inventories.  One of Everett’s hypotheses is that the lower air pressure at higher altitudes makes ejectives easier to produce, and drier climates at higher altitudes “may help to mitigate rates of water vapor loss through exhaled air”.  While I don’t have anything against this kind of theory in principle, and I’m not going to comment on the plausibility of this theory, I wanted to check whether the stats held up.

This sounds suspiciously like one of our spurious correlations – links between cultural features that come about by accidents of cultural history rather than being causally related.  Although Everett notes that the tests he uses include languages from many language families, there’s no real control for historical descent.  James and I have also submitted a paper to PLOS ONE about this phenomenon more generally, and we suggest a few statistical tests that should be applied to this kind of claim.  These include comparing the correlation of the variables of interest with similar variables that you don’t think are related, and controlling for historical descent by using, for example, phylogenetic generalised least squares.  In this post, I apply these tests.

First, I test whether the link between ejectives and elevation is stronger than the link between elevation and many other linguistic features.  I ran a correlation for each variable in the WALS database.  Elevation (altitude) does indeed significantly predict the presence of ejectives.  Surprisingly, only 2 other variables resulted in stronger predictors of elevation.  That is, the presence of ejectives is in the top 1.4% of variables for predicting elevation.  The presence of ejectives resulted in a correlation that was significantly stronger than 94.4% of variables (above 1.98 standard deviations). This is surprisingly good news for Everett!

Below is a histogram of the results (F-score of the model fit), with a red line indicating the strength of the ejectives variable :

The linguistic variables that gave better results than ejectives were the Order of Object and Verb and the Relationship between the Order of Object and Verb and the Order of Adjective and Noun. I can’t think of a good reason that these would be linked.  See below:

The next test involved controlling for common descent of languages.  I built a phylogenetic tree from the linguistic classifications from the Ethnologue.  We’re predicting elevation (continuous) given the presence of ejectives (discrete), so we’ll use a phylogenetic generalised least squares test (you can learn more about doing this at the excellent tutorials by Charles Nunn and others, here).  This weights the observations by how related they are, given a particular model of trait evolution.  The elevation variable has a strong phylogenetic signal (Pagel’s lambda = 0.3, sig. > 0, p<0.00001; sig. different from 1, p<0.00001), so we’ll use Pagel’s covarience matrix.

Surprisingly, the correlation holds up, even when controlling for phylogeny (491 languages, df = 419, residual df = 489, estimated lambda = 0.2787271, coef = 358.9542, t = 3.51, p = 0.0005).  Edit: If you use ejectives as the dependent variable, the result is similar (estimated lambda = 0.8169142, coef = 0.00003975, t = 2.42, p = 0.0157).

I’d like to make two points:  First, this kind of analysis is easy to do, and makes the test more rigorous (I did the above analyses at Singapore airport).  Secondly, while the stats might hold up, this kind of approach can only point towards future research, rather than supplying definitive proof of the hypothesis.  It’s an interesting proposal, and I look forwards to some modelling or experimental evidence.

EDIT:

The phylogenetic tree assumed languages within families evolved over 6,000 years and there was a common ancestor for all language families 60,000 years ago. You can see a diagram of the tree here, with WALS codes.

The altitude data I used comes from the 90-meter NASA database (SRTM3), extracted using the GPS Visualiser, while Everett uses surveys by Google Earth and ArcGIS v. 10.0.  I checked some points and there are very slight differences in the order of a few meters.

There was a debate today between Peter Hagoort and Stephen Levinson on ‘The Myth of Linguistic Diversity”.  Hagoort arguing the case for universalist accounts.  He admitted that language does exhibit a large amount of diversity, but that this diversity is constrained.  He argued that linguistics should be interested in which universal mechanisms explain the boundary conditions for linguistic diversity.  The most likely domain in which to find these mechanisms is the brain.  It comes with internal structure that defines the boundary conditions on the surface structures of human behaviours.  These boundary conditions include the learnability of input, and that language is processed incrementally and under time constraints.  Brains operate under these constraints so that linguistic processing of all languages happens in roughly the same processing stages.  Hagoort argued that proponents of a diversity approach to linguistics think that variation is unbounded or constrained only by culture.  While there is variation between individuals and between languages, it is the general types that we should be focussed on.

In contrast, Levinson suggested that we should be moving away from the picture of the modal individual with a fixed language architecture.  Instead, we should embrace population thinking and recognise the variation inherent at every level of language from typology to processing and brain structures.  While languages are constrained by the processing structures of the brain, these processing structures are plastic and adapt to the language and cultures in which they are embedded.  Adults lose the ability to distinguish sounds that are not part of their language.  Recent work on linguistic planning using eye-tracking shows that the elements of a scene that speakers attend to before starting to speak differs with the canonical word order of their language.  More fundamentally, brain structures can be affected by cultural experience, such as bilingualism or singing (indeed, the effect of bilingualism on processing shows that variation itself is a fundamental constraint).  So, brains do constrain learning and processing, but are themselves subject to constraints from interaction between individuals.  Brains also change over evolutionary time, adapting to a range of pressures.  Therefore, there is a complex ecology of systems that co-evolve to define the constraints on language, and understanding these systems requires focussing on diversity.

Hagoort conceded that there was impressive variation at each level, but wondered what was meant by “fundamental” differences.  For instance, how important is the precise neural architecture of an individual?  Even within the variation pointed out, complex linguistic processing isn’t being done in the thalamus, and this is a constraint that sets a boundary on variation.  Hagoort might have pointed out that, if there was so much variation between individuals, how do they communicate so effectively and how does basic interaction happen so easily between diverse individuals?  This points to brain processing universals that explain the constraints on language.

Both sides agreed that the basic aim of any science, including linguistics, is to discover general principles that explain the data.  However, are researchers focussing on the same data?  What is the object of study that linguistics are trying to find generalisations for?  It seems to me that the debate came down to what each proponent thought was the domain that was most likely to yield general explanations.  Hagoort suggests that we should be focussed on brain structures and processing in the individual.  Levinson, on the other hand, suggests that the interaction between individuals is a key domain (e.g. the interaction engine).  Proponents of cultural evolution such as Simon Kirby might argue that cultural transmission is a key domain.  It’s possible that the most relevant ‘universals’ in each of these domains may be very different.  A constructive step would be to describe how each of these domains constrain the other.  For instance, constraints on language processing in the brain certainly constrain interaction between individuals, but the requirements of interaction may affect how processing is employed.

There were some good points from the floor, including Peter Seuren pointing out that neither view was particularly close to proving their point, since proving universals, or their absence is very difficult.  A paper under review by Steven Piantadosi and Edward Gibson attempts to answer whether it is possible in principle or practice to amass sufficient evidence for a statistical test that would demonstrate a universal.  They conclude that it is possible in principle, but that there are not enough datapoints (languages) in order to achieve the required statistical power.  There was also an appeal for the study of diversity for the sake of diversity – that there are different motivations for explaining phenomena in the world, and that one of them is to understand human diversity.

The general message:  Proponents of universals need to take diversity into account, and proponents of diversity need to be more specific about how diversity maps onto processing and how different domains of language co-evolve.

It’s the unwritten rule of every talk on cultural evolution:  there must be at least one picture of someone whispering into someone else’s ear.  This represents language being passed on from one generation to the next, with the language possibly changing (like in the child’s game broken telephone or chinese whispers).  This classic image often makes an appearance:

However, most are boring old stock images.  So, I’m setting a challenge:  who can find the most awesome ‘broken telephone’ picture?

This is my submission:

Image by Craig Barritt / Getty Images, found at The 45 Most Legendary Pictures Ever Taken.

A paper from the Berkeley economic history laboratory published online last week finds a correlation between speaking a language with grammatical gender distinctions and the economic empowerment of women.  Gay, Santacreu-Vasut and Shoham (2013) find that women in countries with languages that make gender distinctions are less likely to participate in the labour market or politics and less able to get credit or own land.

The study uses a series of regressions to demonstrate robust correlations between grammatical gender and various economic variables from a range of databases.  The gender variables include whether a language has a sex-based gender system, how the genders are used in pronouns, the intensity of the gender system (languages with 2 genders vs languages with 1 or more than 2 genders) and whether gender is assigned semantically or formally.  The correlations control for geographical variables (distance from the equator), climate (tropics, frost days, access to the sea), history of colonisation, continent, religion and cultural beliefs and values.  The findings include statistics such as “Having a sex-based gender system decreases the female labor force participation rate by 13 pp % relative to the base-line value in countries with no gender system”.

The approach is very similar to Keith Chen’s study of future tense and economic savings behaviour, and uses some of the same data including the world atlas of language structures (WALS) and the World Values Survey.  Indeed, Gay et al. find that “women living in countries whose dominant language marks gender more intensively are less likely than men to save”.  The paper follows other studies on the cultural transmission of agricultural technology and the role of women in society (Alesina, Guiliano & Nunn, 2011, see here).

Continue reading “Gender, language and economic power: another spurious correlation?”

This is a guest post by Justin Quillinan (of Chimp Challenge fame).

Cast your reminisce pods back a few days and recall Sean’s iterated learning experiment using the automated transcription of YouTube videos. The process went as follows:

1. Record yourself saying something.
2. Upload the video to YouTube
3. Let it be automatically transcribed (usually takes about 10 minutes for a short video)
4. Record yourself saying the text from the automatic transcription
5. Go to 2

Sean took a short extract from Kafka’s Metamorphosis and found that, as in human iterated learning experiments, both the error rate and compression ratio decreases with successive iterations. He also found that the process resulted in a text with longer and more unique words.

I was curious to see whether we could remove human participants entirely and run computer generated speech through this automated transcription. Here’s the process:

1. Generate an audio file from some text using a speech synthesis program;
2. Generate a transcription of the audio file;
3. Repeat from 1. with the new transcription.

Continue reading “Iterated learning using Youtube videos and speech synthesis”

I recently discovered that videos uploaded to YouTube are automatically transcribed (if they’re in English).  As you might guess, the transcriptions are not perfect, so there will be a discrepancy between what the speaker actually said and what is transcribed.  This is essentially all you need to run an iterated learning experiment (e.g. Kirby, Cornish & Smith, 2008).  Iterated learning is a process of repeatedly transmitting a signal through a bottleneck.  For instance, language is transmitted from adults to children, who learn its rules.  These children then go on to transmit this language to their own children.

Simon Kirby and colleagues have discovered that this process leads to languages becoming both more learnable and more expressive over time.  This happens by the emergence of compositionality: parts of a word become systematically linked to parts of its meaning.  See some posts by Hannah and Wintz on these experiments.

But can we see the same process with non-human learners?  Here’s how iterated learning with YouTube works:

1. Record yourself saying something.
2. Upload the video to YouTube
3. Let it be automatically transcribed (usually takes about 10 minutes for a short video)
4. Record yourself saying the text from the automatic transcription
5. Go to 2

Here’s a diagram of the procedure:

Continue reading “Iterated learning using YouTube videos”

Zach Weinersmith of SMBC comics and various science folk are putting on a Festival of Bad Ad Hoc Hypotheses.  The festival will include presentations of “well-argued and thoroughly researched but completely incorrect evolutionary theory”.  They’re looking for people to give 5 minute presentations.  It takes place at MIT on the 20th April, submissions are due 10th March.

Finally, a place for all our hard work on spurious correlations in culturally evolved systems.

More details here

Yesterday I posted an analysis of some work by Prof. Keith Chen on the link between future tense marking and economic decisions.  Prof. Chen made some suggestions about changes to the analysis, some of which I’ve carried out here.  The new results below indicate that the link between future tense and the propensity to save is more robust than the previous post suggested, which is quite embarrassing, but I submit the findings here anyway.

One of Prof. Chen’s points was that I was using simple linear regression, while his analysis used conditional logit modelling.  This is much more computationally intense, and it’s not feasible for me to run 145 logit models for the given size of dataset (R was telling me it needed 13GB of memory to run an analysis of one linguistic variable! Help, anyone?).

Another suggestion was to look at which linguistic variables explain the residual variation in a model with non-linguistic variables.  That is, controlling for non-linguistic variables such as age, sex and number of children, how much extra variance does a particular linguistic variable account for?

I analysed this by comparing two models for each linguistic variable (using ANOVAS, although the results are equivalent with regressions).  Each model had the propensity to save as the dependent variable and independent variables including age, sex, employment status, marriage status, level of education, religion, number of children and survey year.  The second model also included the linguistic variable.  I then compared the improvement in the model fit using the F-score of the difference in residuals.  (There are some problems here, because different linguistic features will be represented in different sub-sets of the data, but we’ll ignore this for now.)

Continue reading “Whorfian economics reconsidered: Residuals and Causal Graphs”